Engineers account for resonance when designing bridges by predicting a structure’s resonant frequencies before it is built. The currently accepted method for computing damped resonant frequencies was developed in the 1950s and has been the industry standard ever since. However, John W Sanders, associate professor of mechanical engineering at California State University, Fullerton says that he has discovered a faster algorithm, which is more efficient than the standard method because it involves fewer computations. His work was recently published in the journal Nonlinear Dynamics. A follow-up paper is currently under review for publication.
“In computation, speed is king. Given the choice between two algorithms that do the same thing, the faster algorithm is always preferable. This new algorithm could replace the older algorithm currently used in industry to compute resonant frequencies — and it would save computation time.”
To do this, Sanders took inspiration from quantum gravity physics. The two pillars of modern physics are quantum mechanics, which accurately describes nature at extremely small scales, and Einstein’s general theory of relativity, which accurately describes gravity at large scales. Physicists are currently trying to reconcile the two theories, which are mathematically incompatible with one another, Sanders noted.
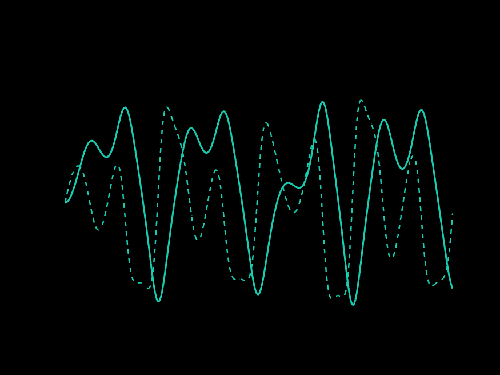
The solid line represents a ‘Duffing oscillator’ while the dotted line represents the associated ‘dual oscillator’ recently discovered by Sanders. The dual oscillator is a key ingredient of the new technique developed by Sanders, which uses fourth-order equations to compute the resonant frequencies of damped systems (John W Sanders).
One of the ways physicists have attempted to solve the problem is by looking at what are called higher-derivative theories. “A derivative is just a rate of change. The velocity of your car, for example, is the rate at which it is moving. The acceleration of your car is the rate at which its velocity is changing. Acceleration is an example of a second-order derivative,” Sanders explained. “The equations that appear in physics tend to involve second-order derivatives like acceleration. A higher-derivative theory might involve a fourth-order equation, for example.”
It was fourth-order equations that caught Sanders’s attention. “I realised that fourth-order equations offer a practical way to handle damping,” said Sanders. “You can basically sweep the damping terms under the rug with a fourth-order equation. You can’t do that with a second-order equation. One immediate application is this new, better way of computing damped resonant frequencies.”
Sanders relayed that his discovery is exciting for a number of reasons. “On a basic level, we now have a much more efficient way to compute the resonant frequencies of damped systems, which is really useful,” he said. “Beyond that, we have made a connection between two seemingly very different fields of study: engineering mechanics and quantum gravity physics. This connection could lead to more discoveries in both fields.”
The research is being presented at noon on Tuesday, 11 October as part of the Pollak Library’s Faculty Noontime Talk Series. To attend, send an email to libadmin@fullerton.edu for the Zoom link, or visit the library’s website here (https://www.library.fullerton.edu/Visiting/programs/2022-fall-faculty-talks.php) for more information.




